在短视频上总可以看到一些让人惊奇的“天才”小孩,譬如下面这个:一个不到5岁的小女孩心算速度堪比计算机。
目前该视频获赞数已突破百万
小女孩是不是很棒!
不过在评论区满满的惊叹和称赞声中,我注意到这样一条留言:
珠心算和手指算,会在上小学后,彻底摧毁孩子的算数能力!
知道为什么嘛?因为每个老师的教学方式都不一样,阻断了孩子的正常思维模式!这样的教育模式太死板,不灵活!上小学你们就知道,毫无用处,还会影响孩子!

每个孩子的成长轨迹不一样,过早的练习心算是否会摧毁孩子的算数能力乃至数学兴趣?我们不得而知,恐怕要等到小女孩再大一点,才可以判断。
但有一个现象是,在中国,许多家长会有意无意地让孩子“早学多学”,生怕孩子输在起跑线上,教育作家黄全愈的儿子亦是如此。
黄全愈的儿子在国内的幼儿园学了不少小学的知识,到美国后,儿子的数学水平已远远超过同班的美国孩子。于是,第一学期结束后,黄全愈向学校申请让儿子插班到三年级上数学课,却被儿子的数学老师拒绝。
老师给出的理由是,“我们的目标是培养孩子成为解决问题的能手,学会思考,让孩子把自信建立在他们自己的能力上,从而去珍视数学。”
当时黄全愈还很不服气,但是13年后,才懂得老师的用苦良心,因为自己的儿子在上大学后,却不再碰数学,尽一切可能避免选修曾经给他带来无数荣耀的数学。
在经过观察后,黄全愈在书中写道,“那些曾经‘大跃进’式学数学、在美国孩子面前大出风头的中国孩子,最终却对数学有敬而远之、甚至产生望“数”生畏的感觉。”
另外一件耐人寻味的事情是,之前著名数学大师丘成桐上《开讲了》节目,现场一名学生问了他一道数学题,丘成桐想了半天答不上来,说“数学家不擅长加减乘除”。
5岁宝宝心算堪比计算器,获得无数教学最高成就的顶尖数学大师却说自己不擅长加减法,这种对比似乎显得颇为诡异和讽刺。

除此之外,数学还充满了其他种种吊诡的“玄学”和“迷思”。
做这个选题时,我咨询了身边很多朋友,有数学成绩好的,不太好的,数学专业的,我把大家对数学的困惑和“迷思”归纳为以下两类。
第一类是针对我这类数学学渣,读书时代被数学虐过千百遍的。
我们会不解:
学数学究竟有什么用?
我们从小背了那么多公式,做了那么多习题,长大后却对那些知识点几乎忘光,现实生活中也几乎用不到勾股定理、三角函数这些枯燥的数学概念,那么学数学究竟有什么意义呢?难道只是吃吃数学的苦,体验它给我们带来的挫败感吗?
第二类是针对那些数学成绩优异,很会做题,也很会拿高分的。
有一个数学专业研究生朋友跟我说:自己被人说“数学很强”说了十多年之后,才发现自己其实根本就没那么喜欢数学,他只是很会遵循指示而已,这让他感到伤心和失败。
那么数学究竟是什么?这个学科到底有什么意义和价值?为什么有些人数学就是学不好?相信我,关于数学的所有困惑、不解乃至憎恨,有很多人都经历过或者正在、将来要经历。
一本名为《一个数学家的叹息》在2019年出版,关于数学的种种“迷思”和批判,该书可谓是让人“大开眼界”。
在本书作者Paul Lockhart看来,数学不仅是一门充满乐趣的学科,它还是一门艺术,只可惜,现有的数学教育摧毁了数学。

数学,
一门被“误解”了的艺术
丘成桐曾在演讲中指出,数学是一门求真求美的学科,Paul Lockhart也秉持类似的观点。Paul认为数学是一门艺术,只可惜我们的文化不认同数学是一门艺术。
Paul在书中如此写道,“我们觉得天文学或物理学很震撼人心,在这一点上,数学完全一样。在天文学家发现黑洞之前,数学家老早就有黑洞的构想了。而且数学比诗、美术或音乐容许更多的表现自由,后者高度依赖这个世界的物理性质,而数学是最纯粹的艺术,同时也最容易受到误解。”

那么,数学这门艺术是如何被误解以及被现代教育所“摧毁”的呢?
作者主要从两个部分解构原因。
首先是学校课堂,Paul用痛心一词来形容学校里的数学教育。
学校教育的目的从来都不在培养学生的思考力和创造力上,学校只是训练小孩的表现,然后可以根据表现将这些小孩分门别类。数学在学校里被毁灭,不应该是太意外的事。
这么丰富且迷人的想象力探索过程,却沦落成一套要死记硬背毫无生气的“事实”。不用说也知道,当年你的数学课有多枯燥,无意义地浪费时间。
譬如我们要求背诵“三角形面积等于底乘以高的一半”,然后在“习题”中反复应用。兴奋之情、乐趣、甚至创造过程会有的痛苦与挫折,全都消磨殆尽了。问题在提出来的同时被解答了——学生没事可做。
当然,作者反对的并不是公式,而是反对这种“拿掉了创造性过程,只留下结果的灌输式方式”。
这导致数学成为一门空壳。
教育者应引导学生提出自己的问题、自己猜测与发现、试错、经历创造中的挫折、产生灵感、拼凑出他们的解释和证明。

其次,是数学课程和教材。
这个所谓的数学课程纲要,最令人震惊的是它的僵化。尤其对高年级学生更是如此。每个学校、每个城市,都用完全同样的方法、完全同样的次序教数学。而大部分的人对这种“老大哥”的掌控,并不感到困扰,只是顺从地接受这种数学课程“标准模板”,把这当作是数学本身。
本来应该是很有意义的题目,可以引导出各种想法、没有界限的讨论与论辩、可是我们却代之以无趣和重复的习题、特定题型的解题技巧,各个主题之间彼此不关联,甚至脱离了数学概念的完整性。
英文老师知道在阅读和写作的情境下学习拼写和发音是最好的;历史老师知道若是拿走事件的背景故事,人名和日期就会很无趣。
唯独数学教育还卡在19世纪,没有进步。
历史上一些最有创造力的人所创造出来的美妙艺术作品——而我们却选择让三流的教科书把它低俗化。目前,我们的数学教材由一套没有历史观点、没有主题连贯性的数学课纲,支离破碎地收集了分类的主题和技巧,依解题程序的难易程度凑合在一起。

这些关于数学的批判和抨击,是不是看得大快人心?
当然,这本书不仅仅停留在控诉,书的后半部分,作者用极为有趣的视角,为我们拆解数学概念。
前方高能预警!
想象一下,你身处于一个充满奇怪生物的丛林。这些生物的行为很有趣,而我想要了解它们,它们是:1,2,3,4,5……
让我们用想象的石头堆来讨论它们。
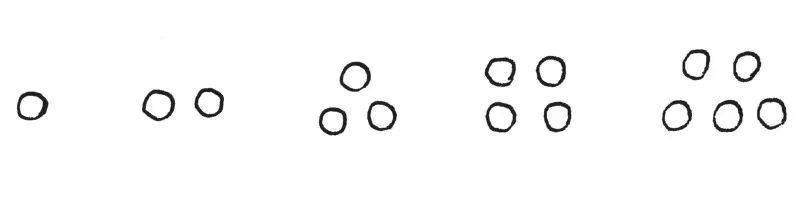
在排列的时候,我们注意到它们之中有些个(石头堆)可以排成两个相等的行列:
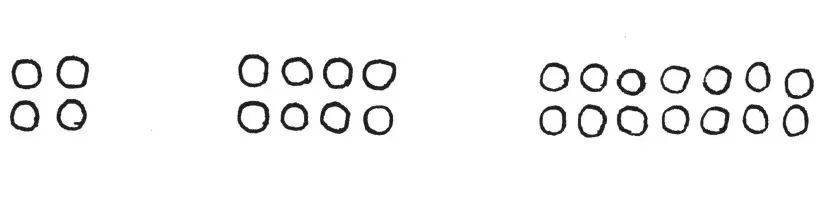
数字2、4、8及14具备这样的属性,而3、5及11则没有。
看出来没有?有些石头堆个性突出,总是有菱角,而有些石头堆温和平滑,由此我们总结出,有菱角的石头堆是奇数,平滑的是偶数。
由于将石头堆推到一起,是我们很自然会去做的事,因此很自然地,我们也会想知道加法对偶数和奇数的区别有什么影响,所以我把这些石头堆摆来弄去一番,结果我注意到一个有趣的模式:
偶数 和 偶数 成为 偶数
偶数 和 奇数 成为 奇数
奇数 和 奇数 成为 偶数
你看出原因了吗?我尤其喜欢两个奇数配在一起的样子:
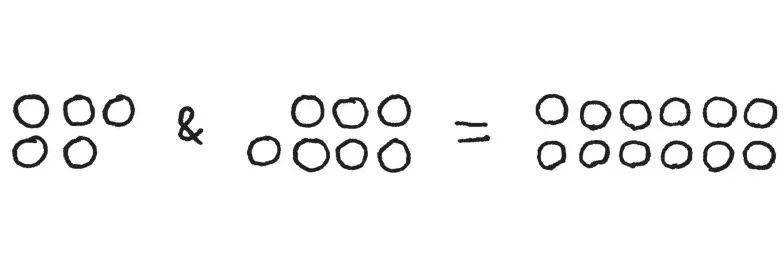
奇妙的“负负得正”特性在此发扬光大。那些恼人的头角正好彼此填平了!
再来!
让我们再次逃回到丛林中,假设丛林里有两只仓鼠。

仓鼠A要跑到仓鼠B,且必须要触碰直线最短的路径是什么?
这是一个多么明确又迷人的题目啊。在不知道这个答案之前,我们会有多种构思。
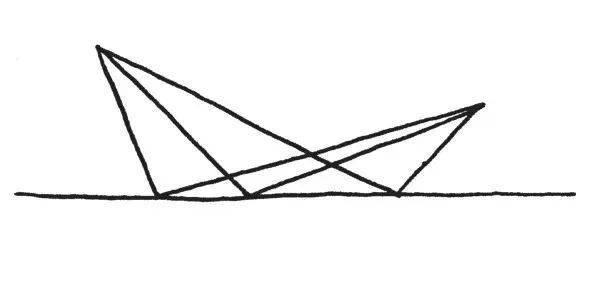
但有一个非常简单的方法,可以告诉我们这条路径是否为最短。这个构想,是几何学当中最令人惊讶和出人意料的构想之一,就是寻找在直线另一侧的镜射(reflection)!
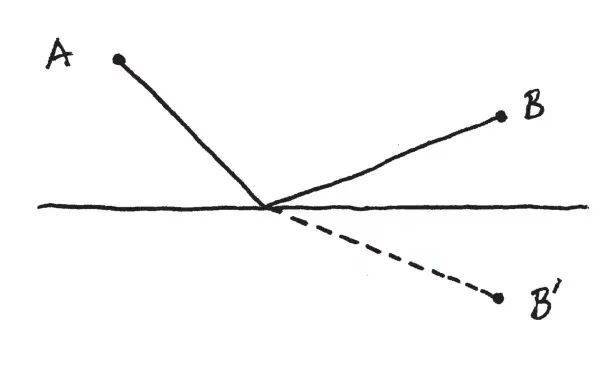
重点来了:新路径的长度和原路径的长度是相同的!这表示,找出从A到B要碰触到直线的最短路径,等于要找出从A到B′的最短路径。但是这容易多了——就是直线呀!换言之,我们要找的路径很简单,就是镜射之后为直线的路径!
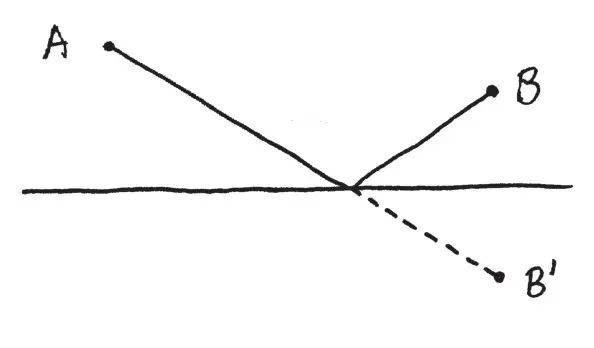
但是这还没有结束。该论证的精髓在于这项事实:跨越直线的镜射,保持住了距离。这表示我们的论证适用于有点、线、距离、镜射观念的任何背景设定。
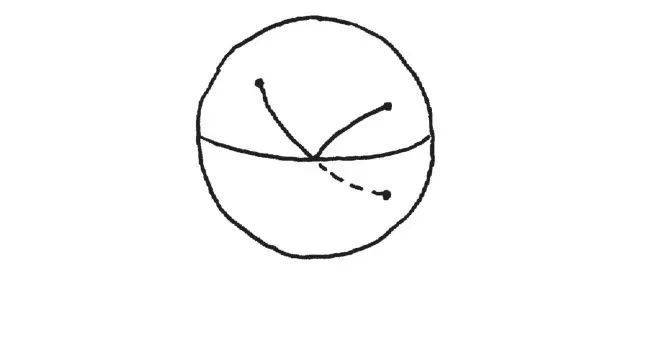
举例来说,在一个球面上,跨越赤道线(equator)有一个镜射的概念:
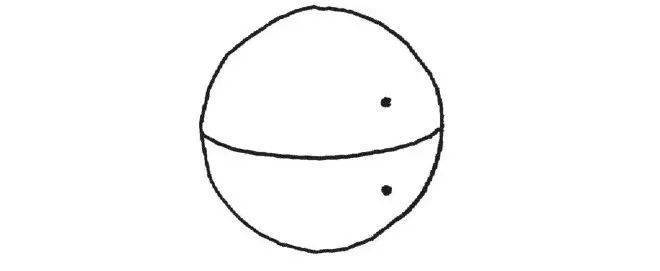
在球面上两个点之间最短的路径,是走赤道线,这也是为什么飞机常采取此航线的原因。
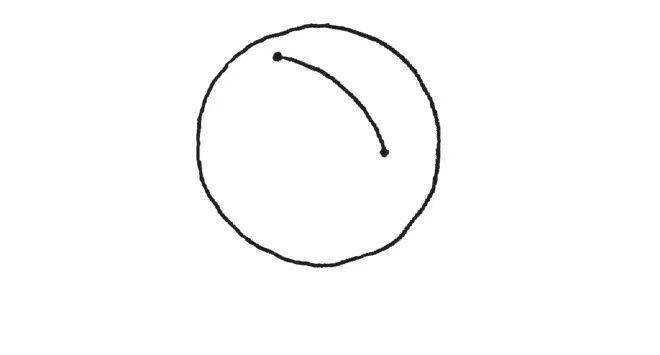
因此,在球面上的相对应题目就会是:在赤道线同一侧的两个点,连接两点并碰触赤道线的最短路径为何?同样的,是与镜射点成直线的路径。
类似的例子,书中还有其它,在书本结尾,作者给读者的忠告是,“数学不需要证照,数学就是玩游戏就对了”。

学数学究竟有什么价值?
遗憾的是,在很多人的学习生涯里,数学给人留下了太多挫败的阴影和不愉快的体验。我们不仅体验不到数学的乐趣,更别提去欣赏它的艺术美感和价值。
作为一个文科生,我对这一点有着深恶痛绝般的感同身受。
其实仔细回想起来,我对数学的敌意和抗拒并非生来俱之,这一点相信很多人都是。整个小学阶段,我也曾因为擅长解题和拿高分被大人夸赞聪明,被老师列为优等生,但是,到了初高中,数学一下成了我的短板和“伤痛”。(转变如何发生的,我后文会讲)尤记得以前每次考完数学发试卷时,都是一场对人格的打压和羞辱。
因为害怕数学,我的本科专业和研究生专业都选择了不用学数学的偏文学类专业。(告诉我我不是一个人!)
因此,在我的经验里,数学除了给人带来恼人的痛苦和羞愧外,似乎没有其它印象和价值了。但当真如此吗?事实上,是我们部分人对数学的无知和刻板印象在“作祟”。
要知道,在北大,数学专业是最难申请的热门专业,丘成桐说他认识很多人靠数学赚了很多钱。不过,从这个角度来评价数学的价值未免显得过于功利,但丘成桐还说过另外一句话:数学是所有学科的基础。没有数学的话,就没有现代的科技社会。数学的美一旦被发现,是可以引领你进入科学殿堂的。
譬如,数学里的共性映射可以应用到表情识别和追踪当中。

用几何分析理论,可以发展成一项虚拟肠镜算法。如今这套算法被普及应用到医学CT影像上,使原本难以在早期被诊断的直肠癌得到有效筛查,并在全世界解救过不少生命。
对了,上面这两个发明都是丘成桐结合数学知识研究所得。
这里再举一个例子。
不知道大家有没有听说过贝尔实验室,它被誉为人类历史上最伟大的实验室(没有之一)。世界上很多伟大的发现都产自于这个实验室。而这得益于学科的交叉和通力合作:很多重大发明都是数学家、物理学家和工程学家一起研究得出的。

图表为贝尔实验室研究成果
丘成桐还说,“数学家的重要性好像一个哲学家,对于整个国家的贡献,你刚开始看不出来,但是长远来讲,整个国家的灵魂都囊括其中。而且纯数学的应用,影响整个国家比哲学快很多。举例来讲,欧洲和美国现在都在研究的领域是量子计算,这里面需要很多纯数学和纯物理的知识。量子力学要是成功,整个工业社会和整个社会科技将被改革。”
不明觉厉,有木有!
当然,普通的孩子,目标不是成为数学家,能够考上北大数学专业的学生更是少之又少,更多的人是在应试教育体制下,尽量多考些分数,当做敲门砖,实现自己其它目标。
如何拿高分,我确实不太擅长。但是通过采访、搜集资料乃至自省过去的经验,我发现了一个非常重要的关键点——很多人的数学兴趣是被无趣的老师所毁掉的!(虽然会出现同一个老师,教出的学生水平不一的情况)
我也算是“深受其害”。
回忆起初一那会,我一上数学课就想睡觉,导致我的数学成绩下降严重,初二换了一个数学老师,普通话标准、声音又好听,那一年,我数学成绩显著提高,一度恢复起对数学的热情和兴趣,但到了初三,又遇到了初一那个老师,数学课再次成为我的“噩梦”,数学成绩不好,导致越学越没自信,也越学越不想学,恶性循环由此形成。
但这又能有什么办法呢?并不是每个学生都那么幸运,可以在重要的时间节点遇到对的“领路人”。
正如Paul所说,文化是自我复制繁衍的怪物:学生从他们老师那里学习数学,而老师又是从他们的老师那里学习数学,所以对于数学欠缺的了解与欣赏,会在我们的文化中无止境地复制下去。

数学究竟该如何学?
还记得我前文所讲的,Paul给大家的忠告吗?数学是艺术也是游戏,是一场探索,是无害并且愉悦的活动。
在这里,我想给大家介绍一位老师Eddie woo,他是一名华裔,被澳大利亚人民誉为数学英雄。

图为Eddie woo与澳大利亚首相Malcolm Turnbull
因为Eddie woo在Youtube上开设了自己的频道,我随意打开几个,下面的评论画风是这样的。

想想一下其他学校的学生都逃掉数学课,但是他们躲到图书馆去看Eddie woo的数学课堂录像。

我有幸亲自上了Eddie woo的数学课,毫无疑问,他向我们展示了教育不仅是一门职业,还是一种启发和唤醒。上帝保佑!
我们必须不惜一切代价保护这个男人。
说Eddie woo掀起了数学革命也不为过,因为有趣的授课方式,很多原本对数学丧失信心和兴趣的学生重新爱上数学。
在2018年,Eddie woo更是被授予2018年度澳大利亚本地英雄奖(Australia's Local Hero for 2018)

怎么让数学这门学科恢复其本真和趣味性,我们需要更多像Eddie woo这样的老师。
目前,Eddie woo的Youtube账号已有114万订阅者,可惜的是这些视频只有英文版本,对于中国学生来说,看懂它确实有语言上的难度。
所谓“兴趣是最好的老师”,建议家长们可以给孩子们读一些数学类的通识读物,培养他们对数学的好奇心,引导孩子们去感受历史上那些群星的动机与目的,不要被人类知识体系中"抽象"的知识和概念吓退。
譬如,这本蒂莫西•高尔斯所著的《数学》就适合初中毕业生看。作者用深入浅出的方式讲诉了很多数学概念。

还有吴军的《数学之美》,这本书就讲诉很多关于数学跨学科的应用。不过,这本书比较适合信息领域大三、大四阶段的学生阅读。读得早了,会因为有些课程没有学过而读不懂,读得迟了恐怕就会感慨怎么没有早点读到这本书。

👆点击图片即可购买👆
总而言之,学习数学需要有一些“数学史”的涉猎与了解。学数学不是拼命地刷题,就算掌握了解题技巧,拿到了高分,倘若我们高中毕业后就远离它,这种教育是充满“叹息”的,这是“数学之殇”。

结语
我写过很多文章,都强调内在驱动力和兴趣的重要性,学习数学亦是如此。
丘成桐是如何成为数学大师的?
在一次采访中,丘成桐讲诉到自己在初二那年遇到了几何,这让他感到很震撼,觉得它又严谨又干净。
之后,他沉浸在几何世界里,就连走在路上和吃饭时也满脑子想着数学。当时,他没有钱买数学书籍,就在图书馆站着看几个小时。
这段描述让我联想到了自己。不过区别是丘成桐是感受到了数学之美,我是为文字之美感到沉醉和震撼。
刚上小学时,我不知道作文为何物,我至今都记得语文老师在课堂上是如何拿着我的作文当作反面教材当着全班同学面批评的,她称我写的是“垃圾”。
直到小学5年级的一天,我在一本书上看到一段话,那是一段很美的排比句,“犹如针扎入血管”般,我体会到文字给人带来的快感和震撼,那段话我当时反复读了很多遍,知道原来文字还可以这么表达,之后像“开窍”了一般,我爱上了阅读,也爱上了写作。
再之后,我因为写作收获过大大小小的成绩。从作文被刊登在学校报纸,到后来去报社实习、做编辑工作、写小说、这些成绩在外人看来或许不足为道,但在我的小小世界里,我自认为找到了可以为之奋斗一生的爱好和“使命”。
这就是兴趣和内在驱动力的巨大力量。
我希望你也有这样内心世界因为某件事被点燃的瞬间和废寝忘食的时刻。
诚然,每个人的驱动力不一样,这里我还想要讲的是,当我们数学怎么学都学不好时,我们有些人会很为沮丧,以为自己的智商不如他人。这种说法显然过于简化和自视甚低。举个例子,有的孩子计算不错,代数就不行;有些代数还不错,但几何就不行。所以,当我们把数学天赋等同于智商时,显然是武断且不正确的。
更何况,有些人虽然数学学不好,可能他又有着其他学科方面的天赋和才华呢?
所以啊,如果数学实在学不好其实也没关系。发现不了数学之美,我们还可以去发掘物理之美、生物之美、文学之美...
标签: 初一作文







